Usually Artificial Intelligence is defined as:
- An attempt to make computers "more intelligent"
- An attempt to understand how humans think

|
Usually Artificial Intelligence is defined as:
|

|
Should we concert reasoning or rather acting of computer systems? Should we take humans as a model or establish new guidelines?
| Systems that Reason | Systems that Act | |
|---|---|---|
| Human model | 1. User Interface problems | 2. Turing Test problems |
| Neo rational | 3. Computationally complex problems | 4. Rational agents/bots |

Approach 1. With this approach, it is not important to solve tasks correctly. It is important to solve tasks in the same way as humans. Applications of this approach include Man-Machine communication and user interfaces.
Approach 2. This approach is rare in AI, however it is the most popular, there are yearly Turing Test competitions.

Approach 3. This logical approach concerns laws of thought. Informal tasks (usually very computationally complex) should be described using a formalism. Applications include expert systems and games.
Approach 4. This approach describes rational agents. These act in the best way to achieve goals, based on their information about the world. The decisions should be taken even if this information is not sufficient. Applications include all kinds of bots.
Any existing human language has the following properties: pretty rich, complex and inconsistent, with a lot of rules and a lot of exceptions. In short, human languages are extremely informal, just like our whole crazy world that these languages try to describe. Constant attempts however are made to teach computers to speak and understand natural languages.

Are "Mikhail Goihman" and "Mikhael (Migo) Goikhman" the same person?
How about "Bill Gates" and "William Gates III"? Or "Peggy Green" and "Green Mary-Ann"?
The problem is more complex than it sounds, because it is not quite formal. One aspect is name nicks and mutations, like:
Peggy -> Margareth -> Martha -> Mary -> Maryanne -> Anna -> Roseanne -> Rosalyn -> Linda -> Melinda
Some aspects may be solved by a database of names and their relations, but there is certainly a place for heuristics. The problem may be even worse in other languages.
use Lingua::EN::MatchNames;
# 85% of certainty
if (name_eq("Leonardo Da Vinci", "Leonard d'Vinchi") >= 85) {
print "Match\n";
}
Games are integral attribute of human beings. They are perfect for learning and fun, develop conscious reaction and satisfy human's thirst of knowledge and curiosity. So, if computers are going to mimic people they should be able to play games.
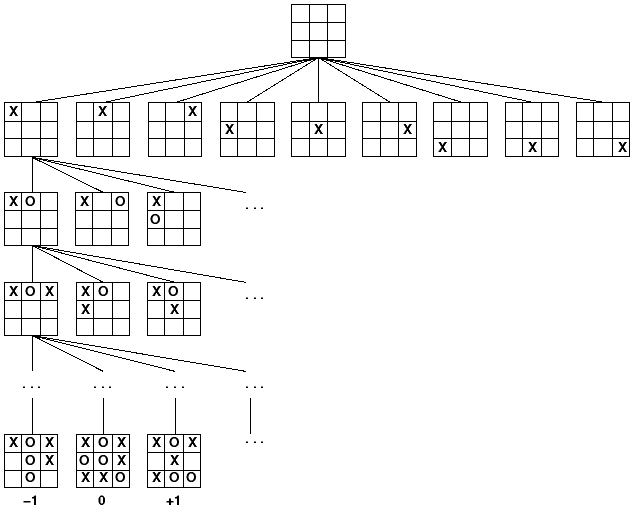
Classical game rules are usually perfectly formalized. The optimal game play is a search of the best next state in the game space, defined by:
Game playing is characterized by:
| Deterministic | Chance element | |
|---|---|---|
| Complete information | 1. Chess, Checkers, Go | 2. Backgammon, monopoly |
| Incomplete information | 3. Card games |
The first type of games is the easiest to approach (but not certainly the easiest to solve). Other types may be approached similarly by adding chance probability nodes that split (multiply) an otherwise deterministic tree of states.
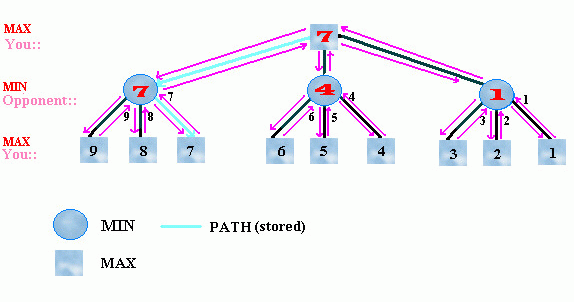
The perfect play for deterministic complete-information games: Choose move to position (one of the immediate tree nodes) with the highest minimax value, i.e. the best achievable payoff against the best opponent play.
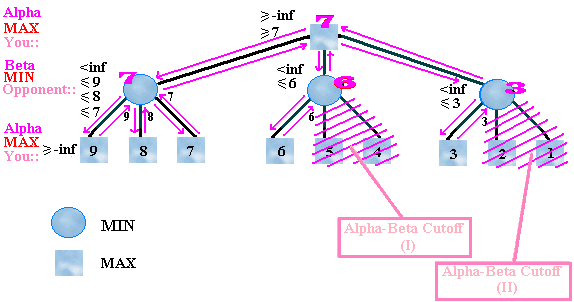
It is possible to skip some subtrees using alpha-beta pruning algorithm:
Minimax algorithm:



In Chess, b (possible moves in typical position) is nearly 40, m (total game play moves) is nearly 100. Typical PC may play like the human master. Deep Blue defeated Garry Kasparov in 1997.
In Checkers on the 8x8 board, a computer program that uses a database of the perfect moves for all positions with 8 or less pieces on the board, is pretty much unbeatable since 1994. International Checkers take place on the 10x10 board. There are Checkers variants with 12x12 and 14x14 boards. The computers will not be able to solve these large boards for many years yet, but they may certainly win an experienced human player.
In Go, b is larger than 300, so the naive minimax approach is not optimal, the pattern based algorithms give better results. Unlike Chess and Checkers, the Go champions refuse to play with computers.
The regular checkerboard is comprised of 64 squares of contrasting colors, like black and white. The checker pieces may be red and white in color (or any combination of contrasting colors), usually grooved.
The black board squares are numbered either 1 to 32 or using the chess a1 to h8 notation. The diagram below shows the pieces set up for play, with Black occupying squares 1 to 12 (lines 6 to 8 in the chess notation) and White occupying squares 21 to 32 (lines 1 to 3 in the chess notation).
Chess notation:
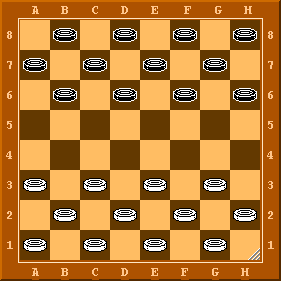
In many countries (and with boards larger than 8x8) the numerical notation is used instead, all black board squares are numbered from 1 to 32.
Each player (White and Black) controls its own army of pieces. Pieces move only on dark squares which are numbered. The white pieces always move first in opening the game.
The goal in the checkers game is either to capture all of the opponent's pieces or to blockade them. If neither player can accomplish the above, the game is a draw.
Starting with White, the players take turns moving one of their own pieces. A piece means either a man (other name is pawn) - an ordinary single checker or a king which is what a man becomes if it reaches the last rank (see kings). A man may move one square diagonally only forward - that is, toward the opponent - onto an empty square.
Checkers rules state that captures or 'jumps' are mandatory. If a square diagonally in front of a man is occupied by an opponent's piece, and if the square beyond that piece in the same direction is empty, the man may 'jump' over the opponent's piece and land on the empty square. The opponent's piece is captured and removed from the board. Some variants allow only forward direction captures, others allow backward direction captures too.
If in the course of single or multiple jumps the man reaches the last rank, becoming a king, the turn shifts to the opponent. No further 'continuation' jump is possible in some variants of Checkers.
When a single piece reaches the last rank of the board by reason of a move, or as the completion of a 'jump', it becomes a king; and that completes the move, or 'jump'.
A king can move in any direction and 'jump' in any direction one or more pieces, as the limits of the board permit. The king can only jump diagonally over one adjacent piece at a time, in any of the four diagonal directions. Multiple jumps are possible.
Games::Checkers is a set of Perl classes and console scripts for automatic and interactive game plays with basic AI. Replay of the recorded games is supported too, and a database of numerous Checkers tournaments is included. Rules for several 8x8 Checkers variants supported. The classes are extendable for GUI.
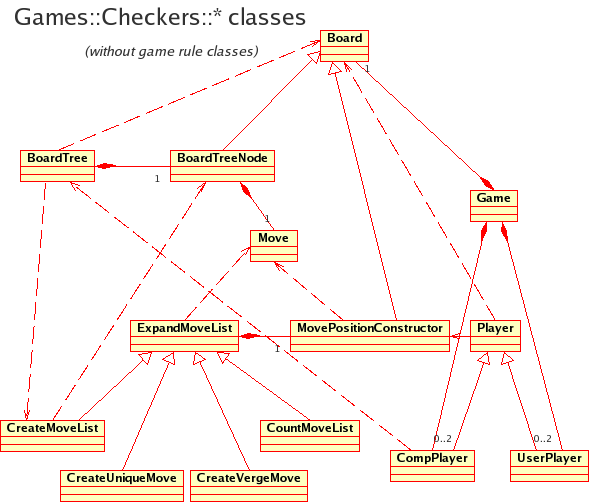
This is a typical class diagram for board based games.
use Games::Checkers::Constants;
use Games::Checkers::Board;
use Games::Checkers::BoardTree;
my $board = new Games::Checkers::Board;
my $color = White;
my $numMoves = 0;
print $board->dump;
while ($board->canColorMove($color)) {
sleep(2);
exit if $numMoves++ == 200; # allow 100 moves for each player
my $boardTree = new Games::Checkers::BoardTree
($board, $color, 2); # think 2 steps ahead
my $move = $boardTree->chooseBestMove; # or: chooseRandomMove
$board->transform($move);
print $move->dump, "\n", $board->dump;
$color = ($color == White)? Black: White;
}
print "\n", ["Black", "White"]->[$color == White? 0: 1], " won.\n";
Perl may be effectivelly used to solve non-CPU intensive AI problems.
Perl is good for prototyping complex AI problems.
Perl is usually not the best choice for computationally complex AI problems.